Einführung
Im 12. Jahrhundert wurde von dem italienischem Mathematiker Leonardo da Pisa
die Fibonaccy Zahlenfolge entdeckt.
Diese Zahlenreihe bestimmt ein wiederkehrendes Muster von Verhältnissen. Dieses Muster ist erstaunlicherweise
in vielen Belangen des täglichen Lebens wiederzufinden.
Da diese Zahlen in menschlichen Handlungsweisen wiederzufinden sind, müssen sie folglich auch in
den Aktienkursen enthalten sein, denn die menschliche Psychologie bestimmt die Aktienkurse.
Diese Bindung zwischen Fibonaccy-Zahlenreihen und Aktienkursen machte sich Ralph Nelson Elliott in
seiner Elliott-Wave-Theorie zu nutze.
Die Fibonaccy Zahlen werden durch eine endlose Zahlenkollne gebildet.
Dabei bildet sich jede Zahl aus der Summe der beiden vorhergehenden Zahlen.
(1=1+0), (2=1+1), 3=2+1, 5=3+2, 8=5+3, 13=8+5,
21=13+8, 34=21+13, 55=34+21, 89=55+34, 144=89+55, 233=144+89
...usw.
dies ergibt die Zahlenfolge:
(0), 1
, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...
Die Formel lautet also:
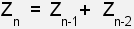
Es gibt zB folgende Auffälligkeiten:
Sonnenblume: hat 89 Blätter, 55 Blätter gehen in die und 34 in
die andere Richtung
Musik: eine Oktave besteht aus 13 Tasten, 5
schwarzen und 8 weißen
|
Es ergeben sich folgende Verhältnisstufen
Division einer Zahl aus der Fibonaccy-Reihe durch die nachfolgende
Zahl ergibt einen Wert nahe der Zahl Pi = 0.618
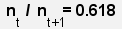
Division einer Zahl der Fibonaccy-Reihe durch die vorangehende
Zahl ergibt einen Wert nahe der Zahl 1+Pi = 1.618
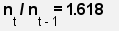
Division einer Zahl der Fibonaccy-Reihe durch die um zwei
Stellen nachfolgende Zahl ergibt einen Wert nahe der Zahl 1-Pi = 0.382
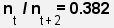
Beispiele:
1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2586 ...
1/2 = 0.5000, 55/89 = 0.6180, 55/144 = 0.3820,
55/233 = 0.2360, 233/89 = 2.6180, 233/55 = 4.2360
0.236, 0.618, 1.618, 0.382, 0.764, 2.618, 0.500, 1.000,
4.236, ...
2.618 x 0.618 = 1.618
0.236 x 4.236 = 1.000
0.618 x 0.618 = 0.382
0.382 x 1.618 = 0.618
|
wichtigsten Fibonacci-Verhältnisse sind:
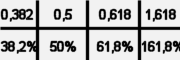
Bei der Technischen Analyse nutzt man nun diese Verhältnisse zum einen bei der
Periodenwahl in der Indikatorenanalyse und zum anderen bei der Kurszielbestimmung.
Bekannte Untergruppen dieser Zyklentechnik sind Fibonacci:
-Extensions
-Retracement Extenions
-Pull Extensions
-Time Extensions (Ratio)
-Time Reverse Time Extensions
-Fanlines
Es erstaunt immer wieder, wie treffsicher die Methode ist.Nuten Sie zB die FibonaccyRetracements
um bereits erarbeitete Unterstützungen/Widerstände erneut zu belegen.Wo diese deckungsgleich
sind, wird die Bestandskraft verstärkt.
Die Fehlerquote der Fibonaccy-Technik ist jedoch nicht zu unterschätzen, da sollte man die
Fibonaccy-Methode mit anderen Techniken der TA gekoppeln.
|
|
